A Taxonomy of Voting Methods

In our series on Choice Architecture, we are exploring how the tectonic plates of governance and technology are colliding in the DAO space. In this second article, we will look at well-known voting methods, before moving on to more exotic crypto varieties in Part 3.

• Default Choices
• Input Space
• Plurality Voting
• Majoritarian Systems
• ∟ Ordinal Voting
• ∟ Cardinal Voting
• Input Space Calculations
• How Should We Delegate?

Default Choices

The first question that choice architects need to make when designing a voting system is whether to offer a default choice that stakeholders are automatically opted into, unless they opt out. Default choices are extremely efficient in uncontentious situations because they allow participants to delegate the default choice to an expert agent, but still preserve decentralization by allowing principals to intervene with an active choice at any time. This has worked well in England and Wales, which have both introduced Presumed Consent for organ donation after death, but still enable citizens to opt-out or families to veto in their place. In a rare display of competence, by reasoning that if a person is not motivated in any direction then the decision is moot, the Government has coordinated tremendous collective action without compromising individual autonomy.

After much experimentation, Aragon Govern has implemented a method of default choice for DAOs, called Optimistic Governance. In this model, the executive agent of a DAO can schedule a transaction with a delayed execution, designed to give anyone the ability to challenge the transaction on the grounds that it goes against any of the rules or principles of the DAO. In this way, the scheduled transaction becomes the default choice that will pass unless explicitly challenged. Because the majority of DAO transactions are uncontroversial, this method eliminates the collective expense of voting in favor of a proposal, but still leaves room for oversight.

The main disadvantage of default choices is that they tend to cede increasing power to the choice architect over time, by not incentivizing participants to educate themselves. One example of this is when utility companies choose not to advise their customers of better tariffs when they become available. This is less heinous than it sounds when the alternative would be a mandate to always maximize customer benefits - a burden that common-law legal systems around the world have consistently rejected. Yet, even if choice architects are not directly to blame, the dynamics of default choices have the potential to entrench an unhealthy paternalism if left unchecked.

One alternative to default choices is to incentivize voting, but this heaps additional costs onto the system, and research has shown that even economic incentives to vote have limited effect compared to default choices.

Input Space

All voting systems are essentially classification algorithms for mapping voter preferences to an output state that may be a single proposition, as in a vote for a president, multiple propositions, as in the composition of a company board, or a composite proposition, as in a government of proportional representation where one’s vote maps to a corresponding percentage of the overall elected body.

The more advanced the algorithm, the more dimensions the ‘input space’ will have and the more nuanced the separation of preferences can be. For example, imagine five voters choosing between three propositions. In this case, there are three options for each voter, meaning that the algorithm has an input space of 3⁵: giving a potential 243 permutations. In practice, the voters might only vote exclusively for one alternative so this serves to restrict the tally to 2/9 of the input space, but not to alter its dimensionality. For the output space, there are two possibilities per proposition - to be chosen, or not - giving us an output space of 2³ - eight permutations, reduced to 3/8 if the propositions are exclusive.

Plurality Voting

The most intuitive voting system is called Plurality voting, where the alternative with the most first-preference votes wins, regardless of whether it achieves an overall majority. In ballots for a single proposition, this is known as ‘First-Past-the-Post’, or ‘Block-Voting’ for multiple propositions.

Because of its simplicity and tendency to elevate stable parties with broad appeal, Plurality Rule is the preferred electoral system for many countries. Unfortunately for those under its census, Plurality Rule is an extremely poor method of capturing sentiment accurately and its dynamics tend to condemn societies to political polarization and long-term two-party rule. This can clearly be seen in the politics of the United States and UK, where two large opposing parties dominate both Parliaments. In fact, this phenomenon is so reliable that it has come to be known as Duverger's law, after Maurice Duverger's 1964 observation that because a vote for an unpopular option is likely to be wasted, rational voters tend to vote for the option closest to their profile that is most likely to win, which ends up favoring the two options that best aggregate the normal distribution of opinion. Henry Droop put it this way as long ago as 1869:

"Each elector has practically a choice between two candidates or sets of candidates .... the electors usually find out that their votes will be thrown away, unless given in favor of one or the other of the parties between whom the election really lies."

There is an argument that Plurality rule improves accountability by limiting the number of agents that can be apportioned blame for a policy misstep, but this is hard to give credence to in a parliamentary system when the disparity between votes cast and seats won can be so extreme: for example, in the 1983 British General Election, the Liberal-Social Democratic Party Alliance won twenty-five percent of the votes, but only three percent of the seats in Parliament.

These extremes occur, not because of the intransigence of voters, but because the voting system itself cannot capture degrees of preference, only crude approximations of opinion. In other words, the input space is not dimensional enough for the algorithm to accurately map the alternatives to voter preferences.

Majoritarian Systems

Majoritarian systems demand a stronger expression of approval from voters by requiring the winning option to secure a majority of the overall tally, not just the most votes. This is achieved by requiring voters to rank or score the options, which vastly increases the input space.

Though magnitudes more representative of voter opinion than Plurality Rule, a ‘tyranny of the majority’ can occur when there is a sizable minority of voters who are strongly opposed to a proposition, but it passes because it is weakly supported by the majority. One defense against the tyranny of the majority is Unanimity Rule, which requires everyone to vote in favor of a proposition before it passes, effectively giving a veto to anyone who disagrees, but this is highly impractical for all but the smallest censuses.

Ordinal Voting

Ordinal voting is a way to augment the input space with extra dimensions to elicit voters’ degree of preference by asking them to rank the options in order. For example, three alternative propositions could be ranked in descending order from ‘1’, being the most favored, to ‘3’, being the least favored. Whereas in the previous example we had an input space of 3⁵, grading each preference on a scale of 1-3 adds another three dimensions, expanding the input space to (3³)⁵, which equals 14,348,907 permutations! Again, the methodology of the vote will restrict the number of permutations to a much smaller subset of the theoretical maximum (by, for example, not allowing voters to mark more than one proposition as their favorite).

If the objective of holding a vote is to form an accurate representation of opinion, then these calculations show how even a modest innovation like Ordinal ranking can capture magnitudes more information.

Condorcet Method

The Condorcet method is a fairness criterion, which states that if there is one option that is ranked higher in every one-to-one comparison with the other options, then, even if it has not achieved a majority, that choice ought to be the winner. On rare occasions, voter preferences may be cyclic such that every option is beaten by at least one other (known as a Condorcet paradox), but this method always guarantees a small subset of options - the Smith set - that beat all others outside the set and from which an overall winner may be chosen. This method is not strictly Majoritarian but rather aims for a consensus of opinion. Its popularity comes from the fact that voting for an unpopular option is not unstrategic.

Borda Count

The Ordinal system most likely to respect the Condorcet winner is the Borda Method or Borda Count. In this system, all options are ranked from n-1 points down to 0 (where n is the number of options) and the option with the most points is the winner. This maximizes the probability that a binary ranking of the candidates is preserved in a group election. As with the Condorcet Method, the Borda Count is designed to elect broadly acceptable options or candidates, rather than those preferred by a majority so is also a consensus-based system.

Cardinal Voting

Cardinal voting adds potentially infinite dimensions to the input space by allowing voters to score their choices (between 1-10 for example). This translates to a much greater potential distance between alternatives in the output space if whole numbers are used and theoretically infinite if fractions are allowed. Importantly, the number of gradations must be greater than the number of candidates, otherwise it becomes de facto Ordinal voting and doesn't contain any extra information.

Cardinal voting is used extensively in non-political contexts, being most familiar to us in online reviews where products are given a star-rating, or sports competitions such as gymnastics where contestants are marked on a cardinal scale for their performance.

The obvious downside of Cardinal voting is that it can easily descend into Ordinal ranking if voters give the maximum score to their preferred alternative, and the minimum score to their least preferred: voting 10-to-0 in favor of one proposition over another on a 0-10 scale is equivalent to voting for 'first' and 'last' in an Ordinal system.

A less obvious quirk of this method is that different voting ranges such as 1-5 or 1-100, even if functionally identical, might be prone to scalar effects and have different symbolic distances in voters' minds, which introduce unknown non-linearities into voting strategies. In general though, Cardinal voting is highly expressive of voter opinion.

Approval Voting

If the Cardinal range is limited to [0,1] or ["Yes","No"], this is known as Approval voting. In theory, this creates the same input space as Plurality voting, but in practice, Plurality voting usually only permits a single choice, whereas each voter may 'approve' any number of options in Approval voting. The winning option is the one with the most support. In setting the voting threshold at the level of mere approval, this method tends to elevate broad, centrist options.

Cumulative Voting

Cumulative voting is Cardinal in nature and an example of fair representation voting, where voters have a restricted number of votes that can be allocated in any permutation across the range of options to signal the degree - as well as direction - of preference. The winning option is the one with the highest number of votes.

In some instances of Cumulative voting, voters will be given vote credits correlated to the number of ballot options, but the method allows for all kinds of credit allocations, including arbitrary round numbers (10, 100, etc) or proportional to shareholding in the case of corporate elections. In each case, the number of vote credits will determine the exponent of the input space and, hence, how expressive the ballot is.

Quadratic Voting

As mentioned, a weakness of Cardinal voting is that it is vulnerable to Ordinal strategies, which dulls its expressive capacity. This phenomenon can occur because there is no cost to the voter when expressing their degree of preference. To combat this effect, a more sophisticated variation on Cumulative voting is Quadratic voting, for which voters must purchase a number of vote credits. To mitigate the outsized influence of wealthy voters, the ratio between credits and votes is quadratic rather than linear. This translates as follows:

• 1 vote = 1 token
• 2 votes = 4 tokens
• 3 votes = 9 tokens
• 10 votes = 100 tokens

The main innovation - and controversy - of Quadratic voting is asking voters explicitly to pay for their votes. Without this, a quadratic relationship between tokens and votes is only a variation on Cumulative voting. The obvious criticism is that the outcome of a Quadratic vote will favor the wealthy, even with quadratic attenuation, so the question is how deleterious this might be to the issue being voted on - something that would have to be assessed on a case-by-case basis.

Input Space Calculations

The following table shows how different voting systems can affect the dimensionality of the input space:

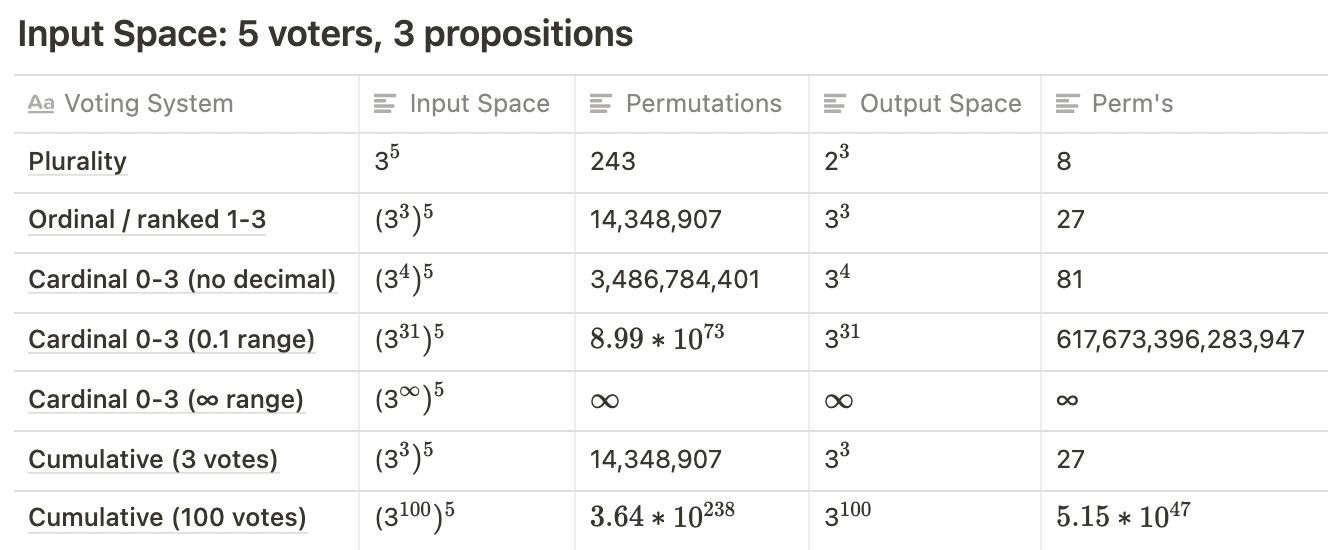
So far, we have only calculated the theoretical maximum size of input spaces, but it is interesting to consider how this is restricted by the actual mechanics of voting.

If x is the number of options and y is the number of credits, then the equation to calculate the number of permutations (p) is as follows if all of the credits must be used (inclusive):

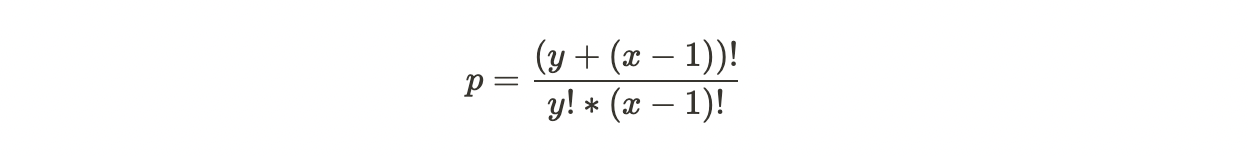
If credits may be wasted (exclusive), then the equation is as follows:

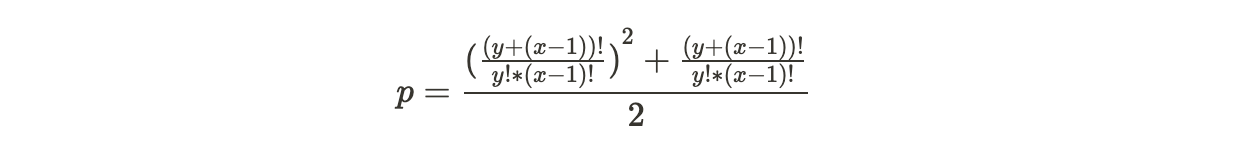
The following table show the effect that this has on the input space and just how much more information may be captured by allowing voters to purposefully waste their votes:

How Should we Delegate?

More than simply augmenting the input space, there are good arguments to suggest that Ordinal voting is the most accurate of all voting methods, despite the larger input spaces enabled by Cardinal voting. From an Austrian economic perspective, every voluntary action is necessarily an expression of ordinal preference (evidently, we rank what we are doing higher than what we aren't doing). This is also how the entire system of voluntary exchange works: if a product ranks higher than its asking price in one's subjective estimation, then one will pay that price and make the exchange. This perspective unravels the paradox of value, whereby diamonds are priced more highly on the market than water, despite water being essential to life: if decision-making were cardinal in nature, no-one would ever exchange diamonds for water, even if they were dying of thirst, but because our decisions are ordinal, in certain circumstances water ranks higher than diamonds. If every decision we make is ordinal, shouldn't our voting methods reflect this?

The answer is that we don't know.. yet. Web3 is a new jurisdiction with novel conventions so what we know of voting might not translate into decentralized organizations. What matters is that DAOs allow us to experiment with a low cost of failure to see what actually works in practice, rather than in principle: governance without politics.